Nama:Vincentius Arianto
NIM:2301921061
NIM:2301921061
Hari:Selasa, 16 Juni 2020
Kelas besar: CB01-CL
Lecturer: Ferdinand Ariandy Luwinda ( D4522 ) dan Henry Chong ( D4460 )
Kelas kecil: LC04-LEC
Lecturer: Julian Wesley ( D5320 ) dan Renaldy ( RX192 )
Linked List
Linked list adalah struktur data yang terdiri dari urutan record data dimana setiap record memliki field yang menyimpan alamat/ referensi dari record selanjutnya (dalam urutan) elemen data yang dihubungkan dengan link pada linked list disebut Node. Biasanya didalam suatu lnked list, terdapat istilah head and tail.
•Head adalah elemen yang berada pada posisi pertama dalam suatu linked list
•Tail adalah element yang berada pada posisis terakhir dalam suatu linked list
Ada Beberapa macam Linked List, yaitu:
1.Single Linked List
Single Linked List merupakan suatu linked list yang hanya memiliki satu varuabel pointer saja. Dimana pointer tersebut menunjuk ke node selanjutnya.Biasanya field pada tail menunjuk ke NULL.
2.Double Linked List
Double Linked List Merupakan suatau linked list yang memiliki dua variabel pointer yaitu pointer yang menunjuk ke node selanjutnya dan pointer yang menunuk ke node sebelumnya. Setiap head dan tailnya juga menunjuk ke NULL .
3.Circular Linked List
Circular Linked List merupakan suatu linked list dimana tail (node terakhir) menunjuk ke head(node pertama).Jadi tidak ada pointer yang menunjuk NULL ada 2 jenis Circular Linked List Yaitu:
• Circular Single Linked List
• Circular Double Linked List
4.Multiple Linked List
Multi Linked List Merupakan Suatu Linked List yang Memiliki Lebih dari 2 buat variabel pointer.
Konsep Stack
-Stack adalah struktur data linear yang dapat diimplementasikan dengan menggunakan array atau linked list.
-Elemen-elemen dalam stack ditambahkan dan dihapus hanya dari satu ujung, yang disebut Top.
-Data disimpan dengan cara Last In First Out (LIFO)
Fungsi dalam Struct
push (x) : tambahkan item x ke atas tumpukan.
pop () : menghapus item dari atas tumpukan.
top () : mengungkapkan / mengembalikan item teratas dari tumpukan.

Kegunaan Stack
Stack banyak digunakan untuk:
-Membalik urutan data
-Mengubah ekspresi infix menjadi postfix
-Mengubah ekspresi postfix menjadi infix
-Sistem Stack digunakan di setiap fungsi rekursif
-Mengonversi angka desimal menjadi angka setara binernya
Queue
Stack banyak digunakan untuk:
-Membalik urutan data
-Mengubah ekspresi infix menjadi postfix
-Mengubah ekspresi postfix menjadi infix
-Sistem Stack digunakan di setiap fungsi rekursif
-Mengonversi angka desimal menjadi angka setara binernya
Queue
Konsep Queue
-Queue dapat diimplementasikan dengan menggunakan array atau Linked list.
-Elemen-elemen dalam antrian ditambahkan di satu ujung yang disebut rear dan dihapus dari ujung yang lain yang disebut front.
-Data disimpan dengan cara First In First Out (FIFO), ini adalah perbedaan utama antara stack dan queue.
Fungsi dalam Queue
push (x) : tambahkan item x ke belakang queue.
pop () : menghapus item dari depan queue.
front () : mengungkapkan / mengembalikan item paling depan dari queue
Hashing and Hash Tables
Hashing
-Hashing is a technique used for storing and retrieving keys in a rapid manner.
-In hashing, a string of characters are transformed into a usually shorter length value or key that represents the original string.
-Hashing is used to index and retrieve items in a database because it is faster to find item using shorter hashed key than to find it using the original value.
-Hashing can also be defined as a concept of distributing keys in an array called a hash table using a predetermined function called hash function.
Hash Table
-Hash table is a table (array) where we store the original string. Index of the table is
the hashed key while the value is the original string.
-The size of hash table is usually several orders of magnitude lower than the total number of
possible string, so several string might have a same hashed-key.
-Hash table is a table (array) where we store the original string. Index of the table is
the hashed key while the value is the original string.
-The size of hash table is usually several orders of magnitude lower than the total number of
possible string, so several string might have a same hashed-key.
Hash Function
There are many ways to hash a string into a key. The following are some of the important
methods for constructing hash functions.
There are many ways to hash a string into a key. The following are some of the important
methods for constructing hash functions.
-Mid-square
-Division (most common)
-Folding
-Digit Extraction
-Rotating Hash
Trees & Binary Tree
Tree Introduction
-A tree is a non-linear data structure that represents the hierarchical relationships
among the data objects
among the data objects
-Some of the tree relations can be observed in directory structures or organizational
hierarchies.
hierarchies.
-The node in the tree need no to be stored contiguously and can be stored anywhere and
linked by pointers
linked by pointers
Tree Concept
Tree is a collection of one or more nodes.
-Node at the top is called as root.
-A line connecting the parent to the child is edge.
-Nodes that do not have children are called leaf.
-Nodes that have the same parent are called sibling.
-Degree of node is the total sub tree of the node.
-Height/Depth is the maximum degree of nodes in a tree.
-If there is a line that connects p to q, then p is called the ancestor of q, and q is
a descendant of p.
a descendant of p.
Tree Example
DEGREE of TREE = 3
DEGREE of C = 2
HEIGHT = 3
PARENT of C = A
CHILDREN of A = B, C, D
SIBLING of F = G
ANCESTOR of F = A, C
DESCENDANT of C = F, G
Binary Tree Concept
-Binary tree is a rooted tree data structure in which each node has at most two children.
-Those two children usually distinguished as left child and right child.
-Node which doesn’t have any child is called leaf.
Type of Binary Tree
-PERFECT binary tree is a binary tree in which every level are at the same depth.
-COMPLETE binary tree is a binary tree in which every level, except possibly the last, is
completely filled, and all nodes are as far left as possible. A perfect binary tree is a complete
binary tree.
completely filled, and all nodes are as far left as possible. A perfect binary tree is a complete
binary tree.
-SKEWED binary tree is a binary tree in which each node has at most one child.
-BALANCED binary tree is a binary tree in which no leaf is much farther away from the root
than any other leaf (different balancing scheme allows different definitions of “much
farther”).
than any other leaf (different balancing scheme allows different definitions of “much
farther”).
Advantages
-It enables linear traversal of elements in the tree
-Linear traversal eliminates the use of stacks which in turn consume a lot of memory space
and computer time
and computer time
-It enables to find the parent of a given element without explicit use of parent pointers
-Since nodes contain pointers to in-order predecessor and successor, the threaded tree
enables forward and backward traversal of the nodes as given by in-order fashion
Tugas membuat program Minimarket dengan double linked list
CPP bisa di download di sini
Balanced Binary Tree (AVL Tree)
AVL Tree adalah sebuah balanced binary search tree yang memiliki perbedaan tinggi
maksimal satu diantara subtree di kiri dan subtree di kanan. AVL Tree digunakan untuk
menyeimbangkan binary search Tree yang tidak seimbang. Dengan menggunakan AVL
Tree, waktu pencarian dalam tree akan lebih cepat karena seimbang.
Cara menentukan tinggi dan Keseimbangan
Tinggi :
- Jika node (root) tidak memiliki subtree tingginya = 0
- Jika node adalah leaf, tinggi = 1
- Jika node internal, maka tinggi = tinggi tertinggi dari anak node + 1
Keseimbangan :
-selisih tinggi diantara anak di kiri dan di kanan, jika node tidak memiliki anak, maka
dianggap 0.
Kalau keseimbangan bukan 1,0, atau -1 maka tidak balance
ada 4 case:
Case 1 : LL the deepest node is located at the left sub tree of the
left child of T.
Case 2 : RR the deepest node is located at the right sub tree of the
right child of T.
Case 3 : RL the deepest node is located at the right sub tree of the
left child of T.
Case 4 : LR the deepest node is located at the left sub tree of the
right child of T.
Jika case 1 and 2 (left-left atau right-right) dibenarkan oleh single rotation.
Jika case 3 and 4 (left-right atau right-left) dibenarkan oleh double rotation.
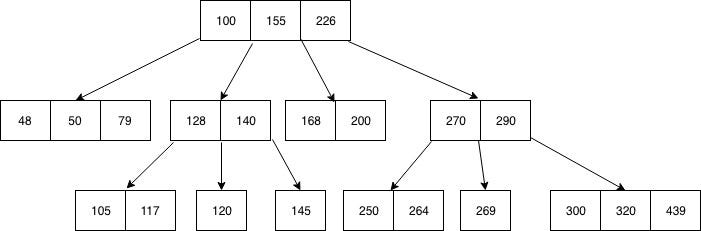
B-Tree
B-Tree atau dikenal istilah order adalah sebuah self balancing search tree.Order
dalam B-Tree menentukan jumlah maksimum/minimum anak yang dimiliki oleh
setiap node. 2-3 Tree merupakan salah satu B-Tree yaitu B-Tree berorder 3. Itu
sebabnya setiap nodenya memiliki batasan anak, dengan minimal 2 anak dan
maksimal 3 anak.
Aturan pada B-Tree : m = order
- Setiap node (kecuali leaf) memiliki anak paling banyak sejumlah m anak
- Setiap node (kecuali root) memiliki anak paling sedikit m/2 anak
- Root memiliki anak minimal 2, selama root bukan leaf
- Jika node non leaf memiliki k anak, maka jumlah data yang tersimpan dalam node k-1
- Data yang tersimpan pada node harus terurut secara inorder
- Semua leaf berada pada level yang sama, level terbawah
Heap dan Tries
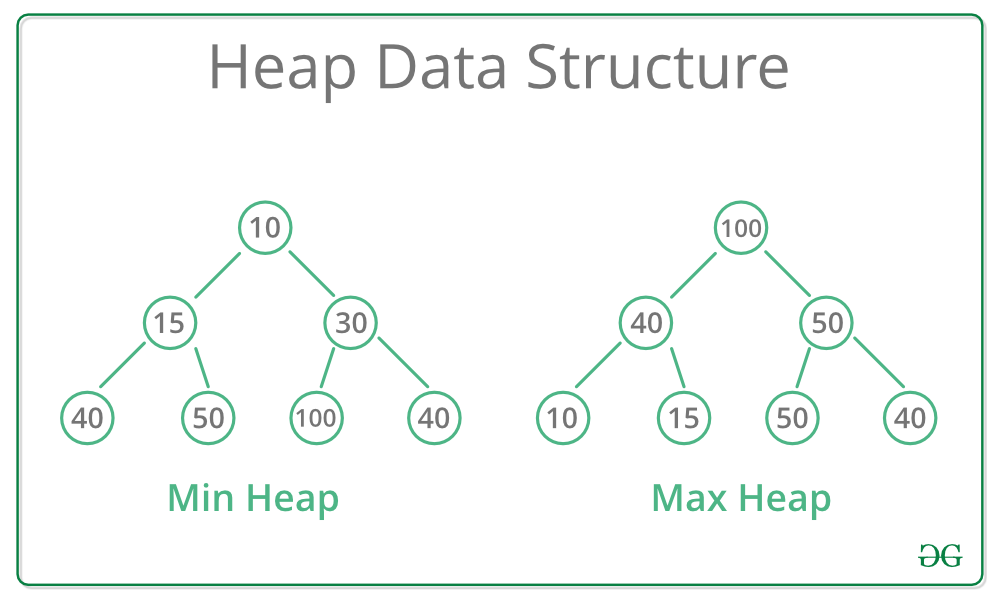
Heap
Heap adalah binary tree komplit yang berbasis struktur data dan memenuhi
aturan heap. Tree pada heap tidak memenuhi aturan binary search tree yang
harus terurut secara inorder, yang penting tree tersebut mengikuti aturan heap.
heap ada 3 jenis:
-Min Heap
Heap dengan Node paling kecil adalah root dan anak nya semakin kebawah
semakin besar.
-Max Heap
Heap dengan Node paling besar adalah root dan anak nya semakin kebawah
semakin kecil.
-Min-Max Heap
Gabungan dari Min Heap dan Max Heap dimana Node paling kecil di root Node
paling besar di anak root terus selang-seling min-max seterusnya.
Tries
Tries (prefix tree) adalah struktur data tree terurut yang digunakan untuk menyimpan array
asosiatif (biasanya string). biasanya digunakan untuk auto complete.